电容元件#
电容元件是电容器的理想化模型。电容元件是一种电荷与电压相约束的电容器的理想化模型 , 具有存储电荷从而在电容器中建立电场的作用。
线性非时变电容元件#
电容元件的特性曲线是 u−q 平面上一条过原点的直线,且不随时间而变化。即,
u(t)q(t)=C(常数)电容元件的 VCR#
在关联参考方向下:
i=dtdq=dtdCu(t)=Cdtdu由此我们可以看出,电容的电流取决于该时刻电容电压的变化率。电容元件是一种动态元件。
电容元件的基本性质#
动态特性#
∣i∣∝⎩⎨⎧dtdu=0→i=0相当于直流dtdu↑→∣i∣↑dtdu↓→∣i∣↓电容在直流电路中相当于开路——隔直作用
记忆性质#
在关联参考方向下:i=Cdtdu。如果我们知道电流求电压,就需要积分:
uc(t)t>t0=C1∫−∞ti(ξ)dξ=C1∫−∞t0i(ξ)dξ+C1∫t0ti(ξ)dξ=uc(t0)+C1∫t0ti(ξ)dξ我们将 uc(t0) 称作初始电压,结论: 在某一时刻的电容电压不仅与该时刻的电流有关 , 而且还与此时刻以前的所有电流值有关。电容电压具有 “ 记忆 “ 性质 ,电 容元件是一种记忆元件。
电容电压的连续性#
设 uc(t0)=uc(0)=0。假设电流按照图示变化: 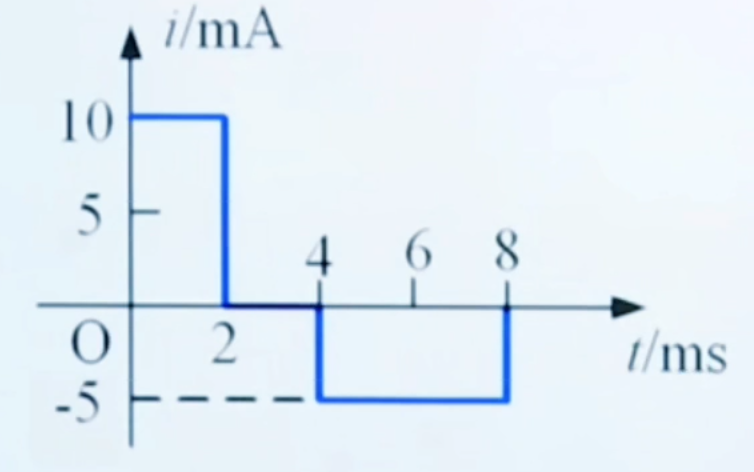 那么根据之前的表达式,可以得到电压的变化:
那么根据之前的表达式,可以得到电压的变化: 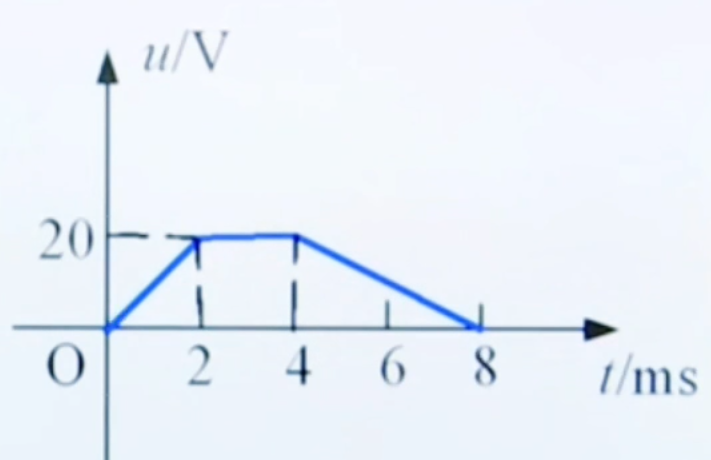 我们可以看出电容电流波形虽然不连续 , 但电容电压波形却是连续的。因此,在电容电流为有界值的情况下,电容电压不能跃变。
我们可以看出电容电流波形虽然不连续 , 但电容电压波形却是连续的。因此,在电容电流为有界值的情况下,电容电压不能跃变。
无源性#
在某时刻电容的储能只与该时刻的电压有关,电容的储能总为正。电容是无源元件。
电容元件的串并联#
电容元件的串联#
n 个电容元件串联,其可以用一个等效电容来替代,其等效电容 Cs 满足:
Cs1=C11+C21+⋯+Cn1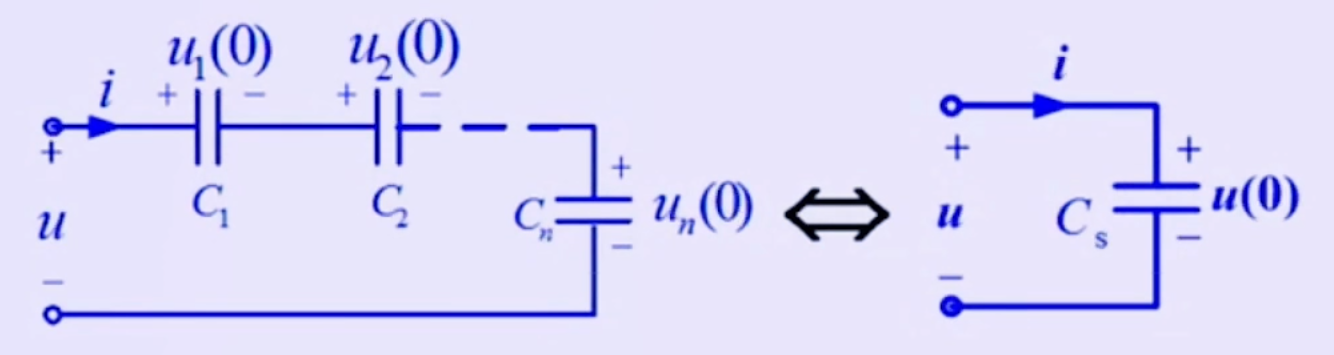
电容元件的并联#
n 个电容元件并联,也可以用一个电容元件等效替代,其等效电容 Cp 满足:
Cp=C1+C2+⋯+Cn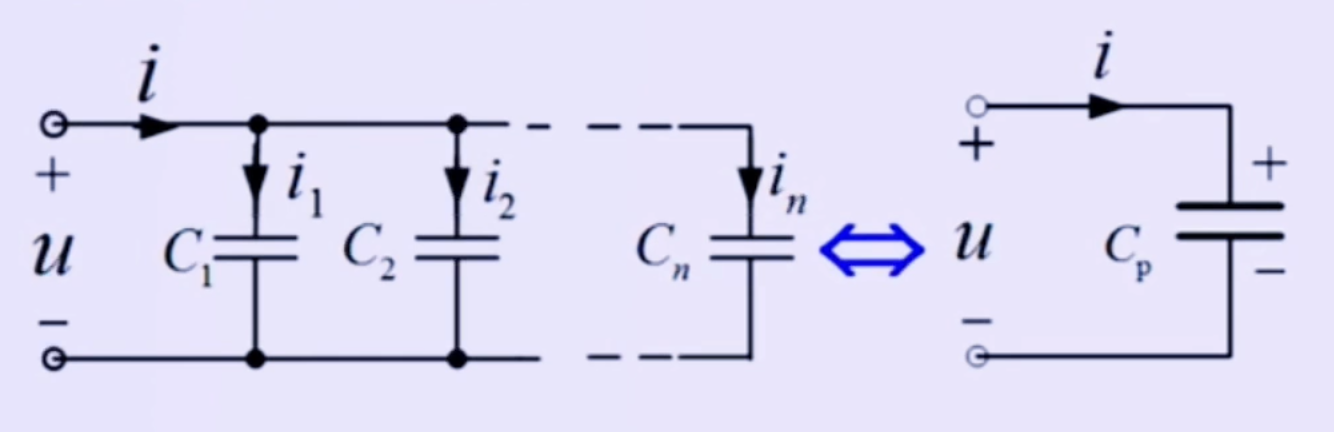
电感元件#
电感元件是电感器的理想化模型。
线性非时变电感元件#
电感元件的特性曲线是 i−ψ 平面上一条过原点的直线,且不随时间变化,即:
i(t)ψ(t)=L(L为常数)电感元件的 VCR#
在关联参考方向下:
u=dtdψ=Ldtdi由此我们可以观察出,电感的电压取决于该时刻电感电流的变化率。电感元件是一种动态元件。
电感元件的基本性质#
动态特性#
∣u∣∝dtdi⎩⎨⎧dtdi=0→u=0(相当于直流)dtdi↑→∣u∣↑dtdi↓→∣U∣↓记忆性质#
在关联参考方向下: 如果我们已知电压求电流就会得到这个积分式:
i(t)t>t0=L1∫−∞tu(ξ)dξ=L1∫−∞t0u(ξ)dξ+L1∫t0tu(ξ)dξ=i(t0)+L1∫t0tu(ξ)dξ我们称 i(t0) 为电感的初始电流。由此我们可以看出:某一时刻的电感电流不仅与该时刻的电压有关,而且还与此时刻之前所有的电压值有关。电感电流具有记忆性质,电感元件是一种记忆元件。
电感电流的连续性#
在电感电压为有界值的情况下,电感电流不能跃变——电感电流的连续性。
无源性#
某时刻电感的储能只与该时刻的电流有关,电感的储能总为正。电感是无源元件。
电感元件的串并联#
电感元件的串联#
n 个串联的电感元件可以用一个等效电感元件替代,其中等效电感 Ls 满足:
Ls=L1+L2+⋯+Ln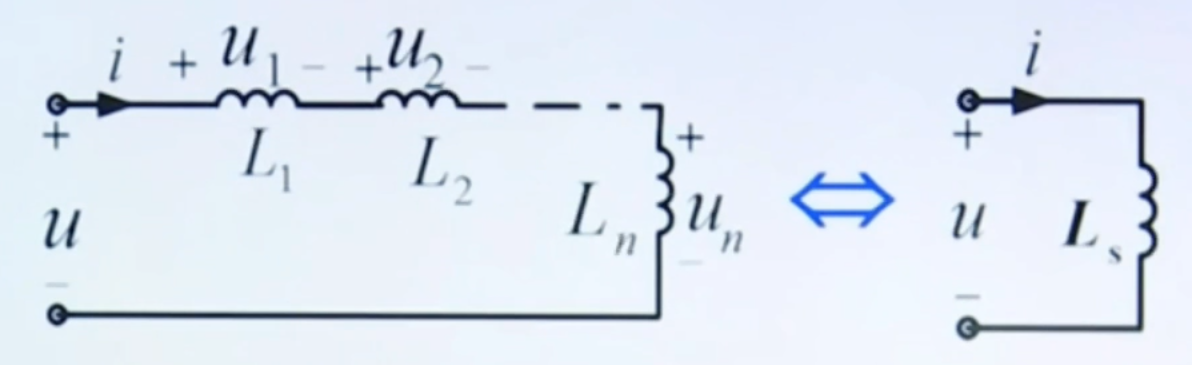
电感元件的并联#
n 个电感元件并联,也可以用一个等效电感元件替代,其中等效电感 Lp 满足:
Lp1=L11+L21+⋯+Ln1换路定则及初始值的确定#
基本概念#
- 换路:由于某种原因(如电源或某部分电路的接通与断开,电路元件参数的改变等)使电路的工作状态发生变化,使其由某一种工作状态变化为另一种工作状态,将这种工作状态的改变称为换路。
- 过渡过程:换路过程中,电路的电量随时间变化的过程称为过渡过程或瞬态。
- 初始值:电量在换路后瞬间的值。
- 换路时刻:t=0, 换路前:t=0−, 换路后:t=0+
换路定则#
在电容电流与电感电压为有界值的的情况下,电容电压不能跃变,电感电流不能跃变。即:
{uc(0+)=uc(0−)iL(0+)=iL(0−)初始值的确定#
- 由 0− 时刻的等效电路计算 uc(0−) 和 iL(0−)。在直流激励下,电容相当于开路,电感相当于短路。
- 根据换路定则确定 uc(0+),iL(0+).
- 由 0+ 时刻的等效电路计算其他各电量的初始值。在 0+ 等效电路中电容用电压值等于 uc(0+) 的电压源替代。电感用电流值等于 iL(0+) 的电流源替代。
动态电路#
基本概念#
- 状态变量:如果已知该量在初始时刻的值,则根据该时刻的输入就能确定电路中任何量在随后时刻的值,称具有这种性质的量为状态变量。电容电压与电感电流就是状态变量。
- 动态电路:至少含有一个动态元件的电路。
- 一节动态电路:用一阶微分方程描述的电路就是一阶动态电路。
- 零输入响应 (z.i.r):在没有外加激励作用下,仅有动态元件的初始储能产生的响应。
- 零状态响应 (z.s.r):动态元件的初始储能为零,仅有外加激励产生的响应。
- 全响应 (c.r
- ):零输入响应与零状态响应之和。
- 时间常数:一阶 RC 电路中: τ=RC. 一阶 RL 电路中,τ=RL 。电压、电流衰减的快慢取决时间常数的大小 τ 越大 , 衰减越慢 , 反之则越快。
一阶 RC 电路的零输入响应#
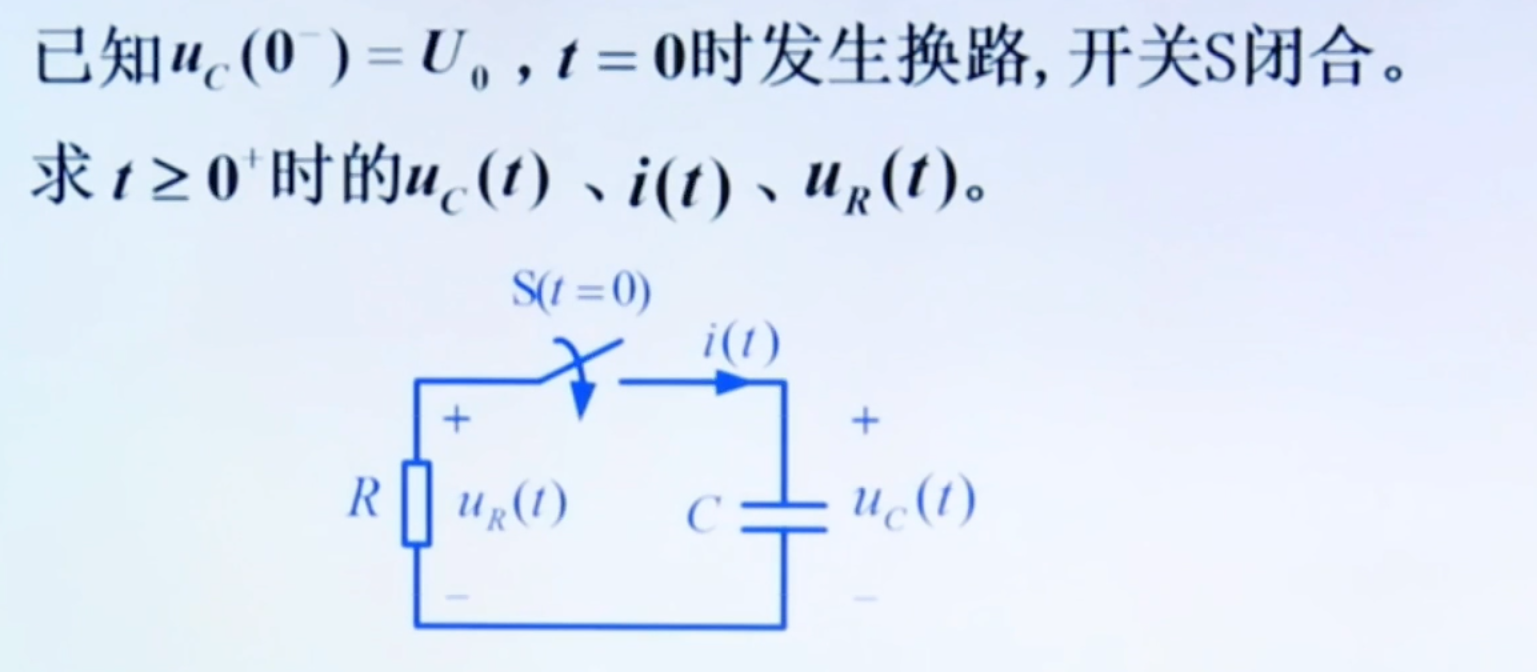
uR−ucuR=−iR,i=0=Cdtdu两式联立,就可以得到一个一阶常系数线性齐次微分方程:
RCdtduc+uc=0,t≥0+通过解微分方程,我们就可以得到:
uc(t)i(t)=U0e−RC1t=uc(0+)e−RC1t,t≥0+=Cdtdu=CU0(−RC1)e−RC1t=−RU0e−RC1t,t≥0+画出图像: 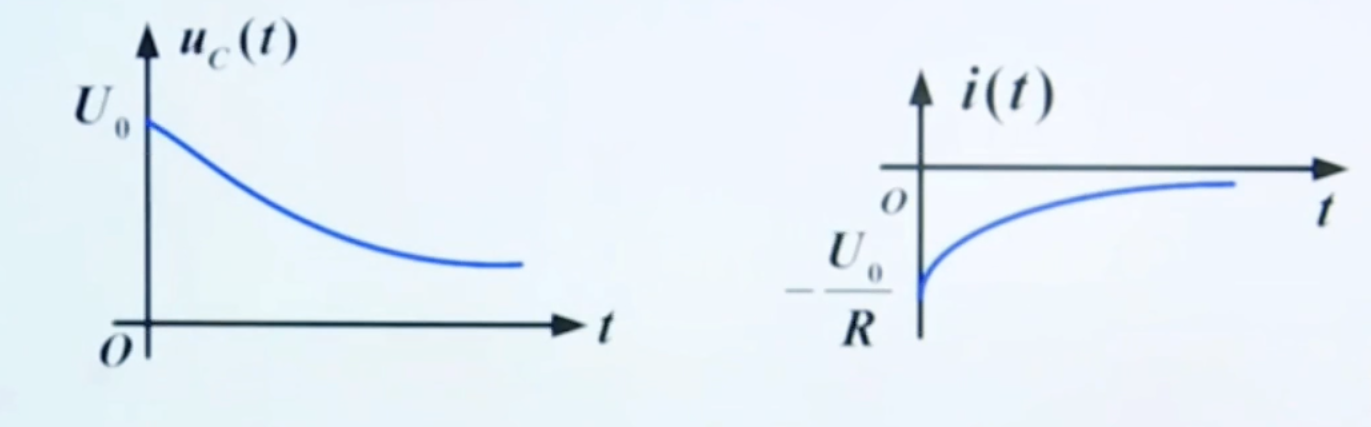 由此可见,一阶 RC 电路的零输入响应是一个放电过程。其中,我们令 s=−RC1=−τ1, 称为 RC 电路的固有频率。由此我们也可以写出零输入响应的标准形式:
由此可见,一阶 RC 电路的零输入响应是一个放电过程。其中,我们令 s=−RC1=−τ1, 称为 RC 电路的固有频率。由此我们也可以写出零输入响应的标准形式:
y(t)=y(0+)e−τt,t≥0+因此我们可以得到结论:只要知道了某量的初始值和电路的时间常数,就能得到该量在过渡过程中的变化规律。
一阶 RL 电路的零输入响应#
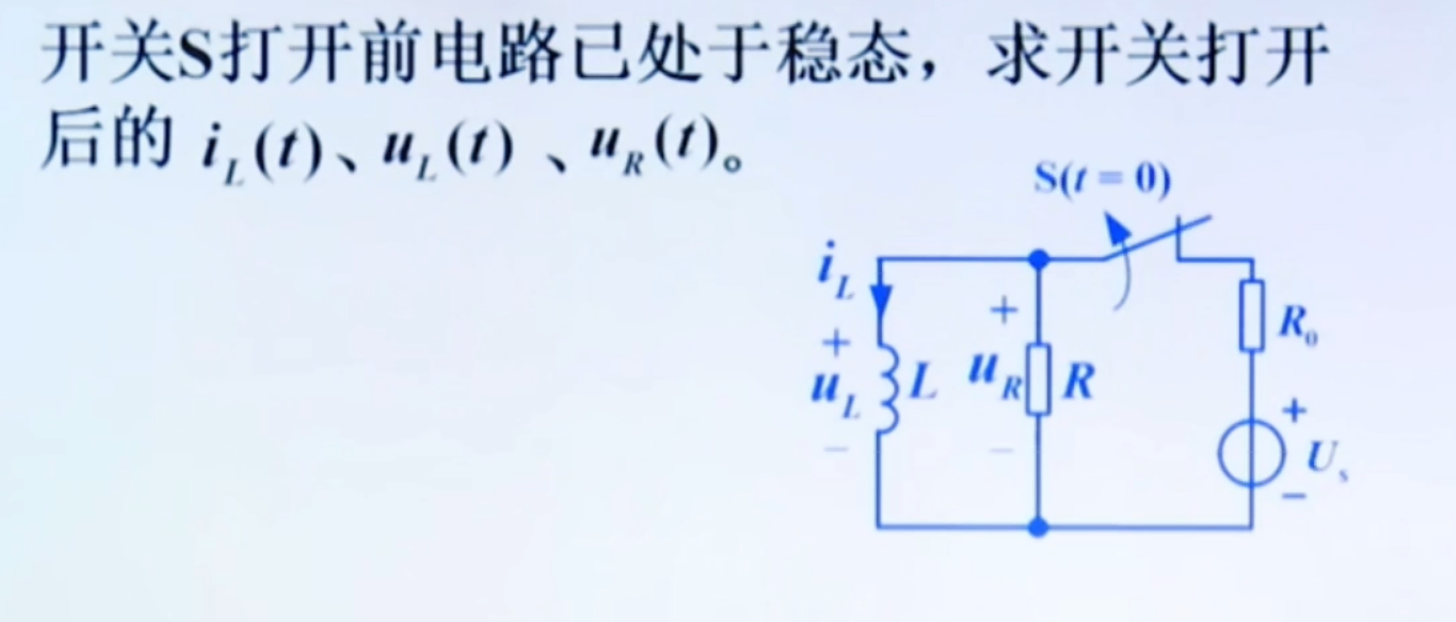 方法与之前类似,最后我们可以求出:
方法与之前类似,最后我们可以求出:
iL(t)uL(t)uR(t)=I0e−LRt=LdtdiL=LI0(−LR)e−LRt=−I0Re−LRt=uL(t)=−I0Re−LRt画出变化曲线: 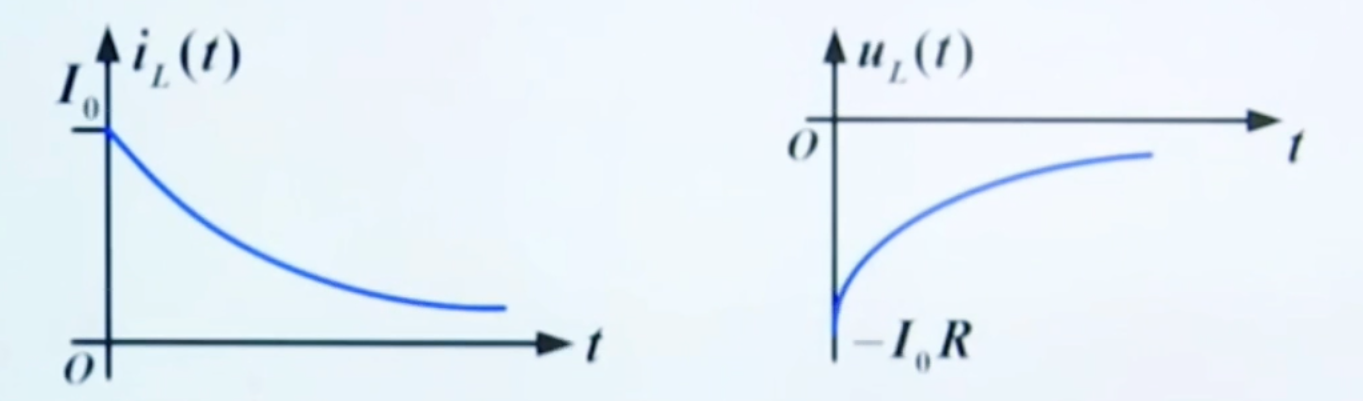 由此可见,一阶 RL 电路的零输入响应是一个放电过程。令 s=−LR=−τ1, 称其为 RL 电路的固有频率。我们就可以写出电路中各量的零输入响应的标准形式:
由此可见,一阶 RL 电路的零输入响应是一个放电过程。令 s=−LR=−τ1, 称其为 RL 电路的固有频率。我们就可以写出电路中各量的零输入响应的标准形式:
y(t)=y(0+)e−τt,t≥0+因此我们可以得到结论:只要知道了某量的初始值和电路的时间常数,就能得到该量在过渡过程中的变化规律。
一阶 RC 电路的零状态响应#
以该电路为例: 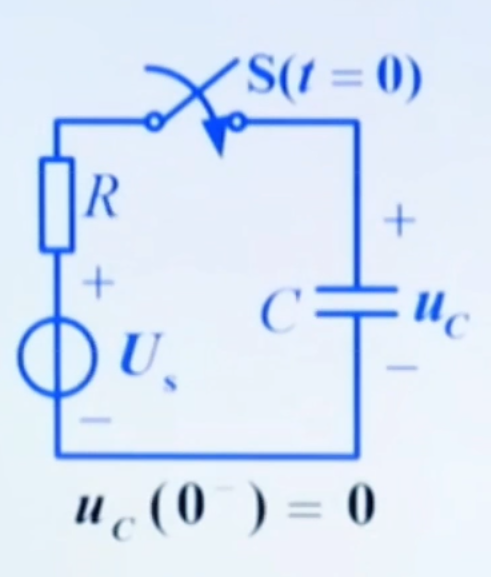 在开关闭合前,电容没有初始储能,即 uc(0−)=0,在 t=0 时刻开关闭合,即得到下面的电路:
在开关闭合前,电容没有初始储能,即 uc(0−)=0,在 t=0 时刻开关闭合,即得到下面的电路: 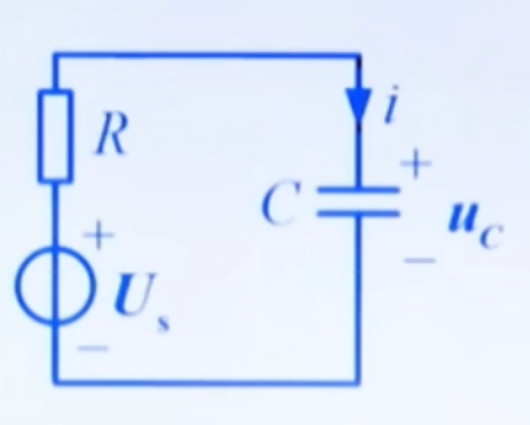 列出 KVL 方程,即:
列出 KVL 方程,即:
t=0+Ri+uc=Us将电流 i 用电容表示,就得到:
RCdtduc+uc=Us,t≥0+这是一个一阶线性常系数非齐次微分方程,对该方程求解,得到:
uc(t)=−Use−RC1t+Us,t≥0+又可以写为:uc(t)=Us(1−e−RC1t),t≥0+从而求得it为:it=RUse−τ1t时间常数 τ=RC,固有频率 s=−RC1。 画出其变化曲线: 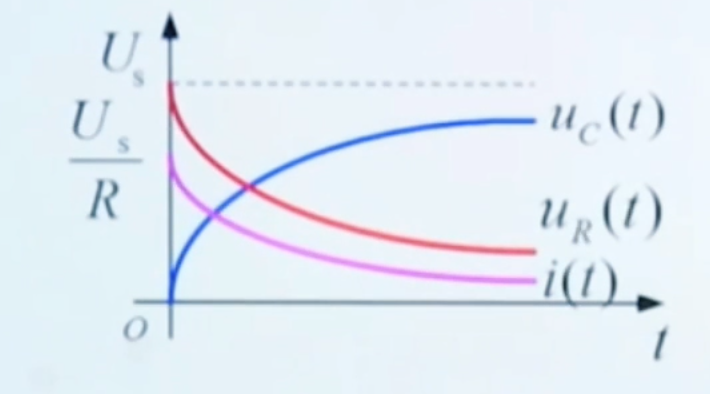 由此我们可以得出:一阶 RC电路的零状态响应是储能从无到有的建立过程,即充电过程。
由此我们可以得出:一阶 RC电路的零状态响应是储能从无到有的建立过程,即充电过程。
一阶 RL 电路的零状态响应#
以该电路为例: 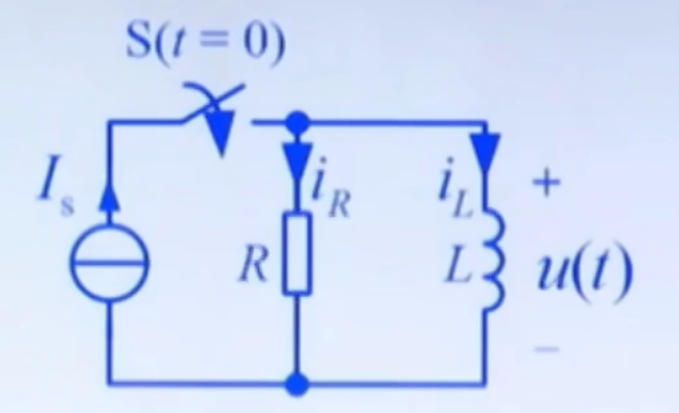 方法与之前类似,我们可以得出以下关系:
方法与之前类似,我们可以得出以下关系:
iL(t)=Is(1−e−LRt)=Is(1−e−τt)u(t)=iR(t)=IsRe−τt时间常数 τ=RL ,固有频率:s=−LR 画出其变化曲线: 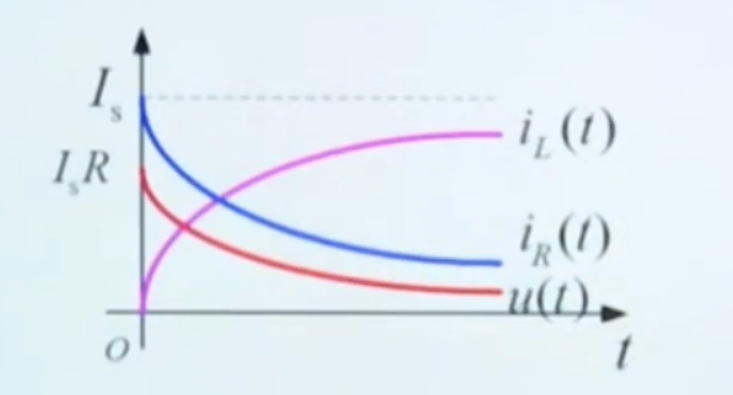 由此我们可以得出:一阶 RL 电路的零状态响应是储能从无到有的建立过程,即充电过程。
由此我们可以得出:一阶 RL 电路的零状态响应是储能从无到有的建立过程,即充电过程。
状态变量的零状态响应的一般形式#
y(t)=y(∞)(1−e−τt),t≥0+零输入响应满足齐次性与叠加性。
一阶电路的全响应#
以该电路为例: 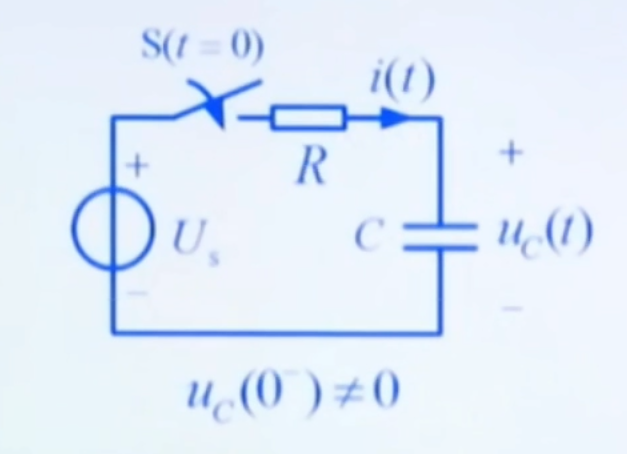
全响应=零输入响应+零状态响应 对于该电路来说:
uc(t)=uCz.i.r(t)+uCz.s.r(t)=uC(0+)e−τt+Us(1−e−τt)一阶电路的三要素法#
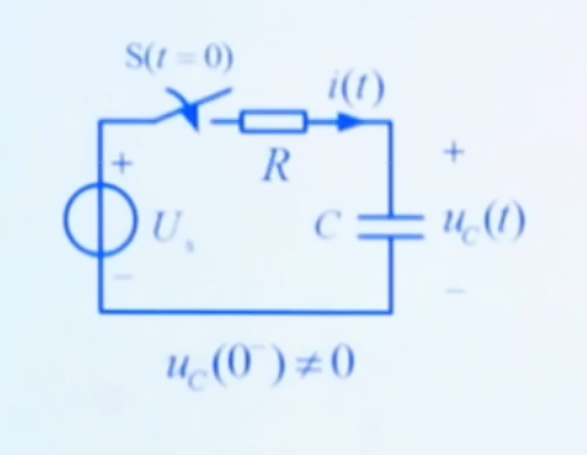 我们之前已经可以用经典的方法(解方程)来得到电容电压:
我们之前已经可以用经典的方法(解方程)来得到电容电压:
uc(t)uc(t)=uCh(t)+uCp(t)=[uc(0+)−Us]e−τt+Us又因为 uCp(t)=Us=uc(∞)(稳态值),A=uc(0+)−Us=uc(0+)−uc(∞) (初始值), 我们就可以得到:
uc(t)=uc(∞)+[uc(0+)−uc(∞)]e−τt在这个式子中,共有三个量:稳态值,初始值以及时间常数。因此,我们只要知道了这三个量,我们就可以求解电路中的任意量,该方法即为三要素法。下面写出三要素法的一般形式:
y(t)=y(∞)+[y(0+)−y(∞)]e−τt三要素的求解#
初值 y(0+)#
- 画 0− 时等效电路,求出 uc(0−)或iL(0−) (此时电容开路,电感短路)
- 画 0+ 等效电路,求出 y(0+)(此时电容用电压值为 uc(0+)=uc(0−) 的电压源替代,电感用电流值为 iL(0+)=iL(0−) 的电流源替代)。
稳态值 y(∞)#
画 ∞ 时等效电路,求出 y(∞)。(此时电容开路,电感短路)。
时间常数 τ#
求 t≥0+ 时,除去动态元件后的含源单口网络的戴维南等效电阻或诺顿等效电阻 Req。
τ=ReqC或τ=ReqL 那么根据之前的表达式,可以得到电压的变化:
那么根据之前的表达式,可以得到电压的变化:  我们可以看出电容电流波形虽然不连续 , 但电容电压波形却是连续的。因此,在电容电流为有界值的情况下,电容电压不能跃变。
我们可以看出电容电流波形虽然不连续 , 但电容电压波形却是连续的。因此,在电容电流为有界值的情况下,电容电压不能跃变。

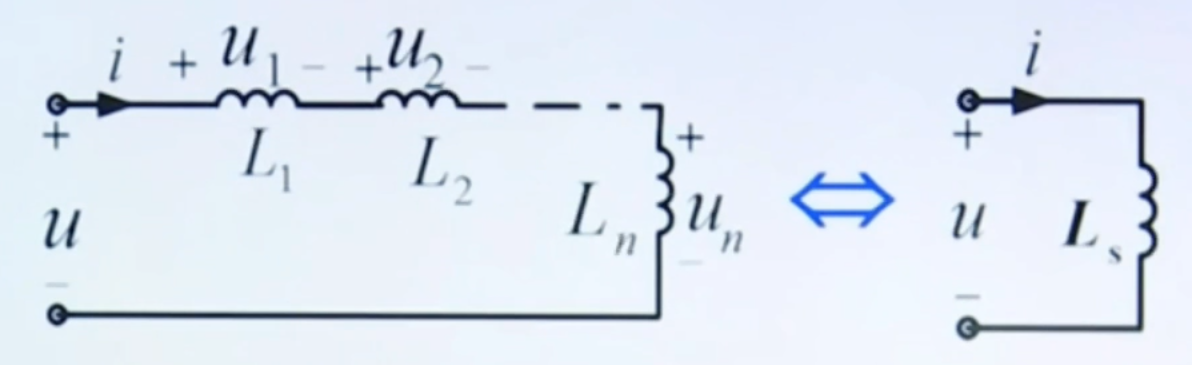

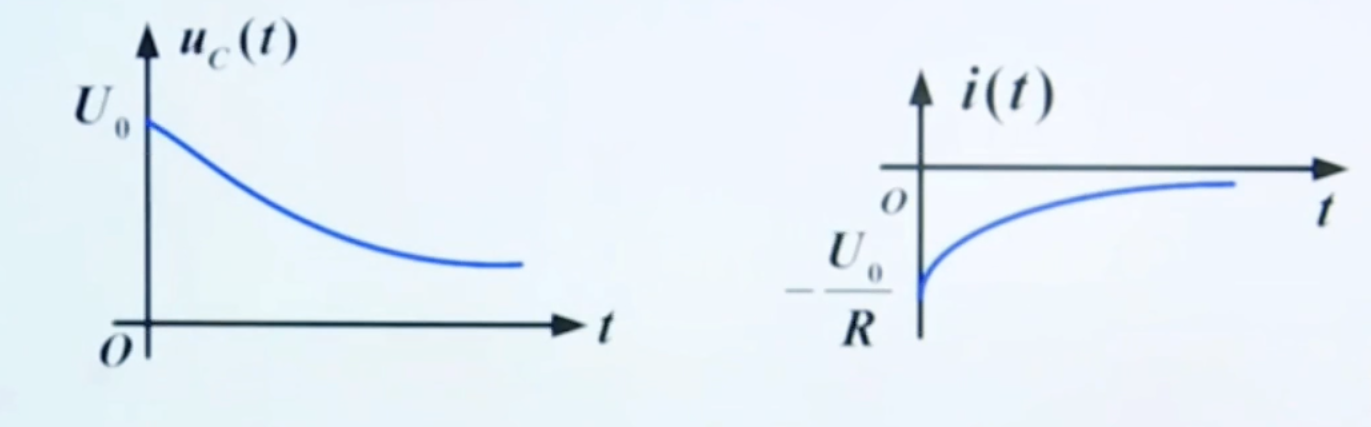 由此可见,一阶 RC 电路的零输入响应是一个放电过程。其中,我们令 , 称为 RC 电路的固有频率。由此我们也可以写出零输入响应的标准形式:
由此可见,一阶 RC 电路的零输入响应是一个放电过程。其中,我们令 , 称为 RC 电路的固有频率。由此我们也可以写出零输入响应的标准形式: 方法与之前类似,最后我们可以求出:
方法与之前类似,最后我们可以求出: 由此可见,一阶 RL 电路的零输入响应是一个放电过程。令 , 称其为 RL 电路的固有频率。我们就可以写出电路中各量的零输入响应的标准形式:
由此可见,一阶 RL 电路的零输入响应是一个放电过程。令 , 称其为 RL 电路的固有频率。我们就可以写出电路中各量的零输入响应的标准形式: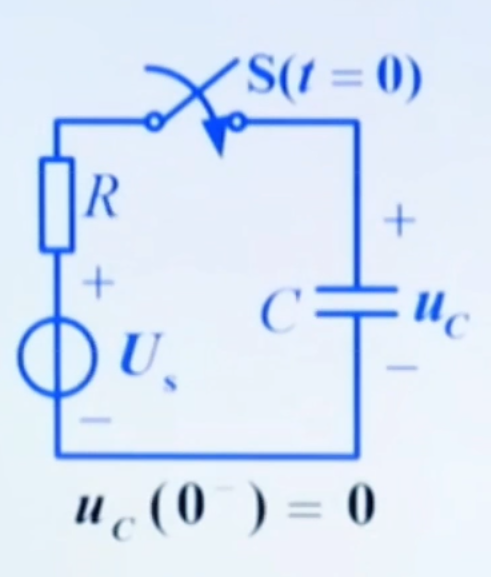 在开关闭合前,电容没有初始储能,即 ,在 时刻开关闭合,即得到下面的电路:
在开关闭合前,电容没有初始储能,即 ,在 时刻开关闭合,即得到下面的电路:  列出 KVL 方程,即:
列出 KVL 方程,即: 由此我们可以得出:一阶 RC电路的零状态响应是储能从无到有的建立过程,即充电过程。
由此我们可以得出:一阶 RC电路的零状态响应是储能从无到有的建立过程,即充电过程。 方法与之前类似,我们可以得出以下关系:
方法与之前类似,我们可以得出以下关系: 由此我们可以得出:一阶 RL 电路的零状态响应是储能从无到有的建立过程,即充电过程。
由此我们可以得出:一阶 RL 电路的零状态响应是储能从无到有的建立过程,即充电过程。
 我们之前已经可以用经典的方法(解方程)来得到电容电压:
我们之前已经可以用经典的方法(解方程)来得到电容电压: