正弦量
正弦量的三要素
正弦量指随时间按正弦规律变化的量。
时域表示:f(t)=Fmcos(ωt+ψ)。其中 Fm 称为振幅,ω=dtd(ωt+ψ) 称为角频率。ψ 为初相位或初相角,简称为初相。其值在 ±π 内。初相反映了正弦量初始值的大小。
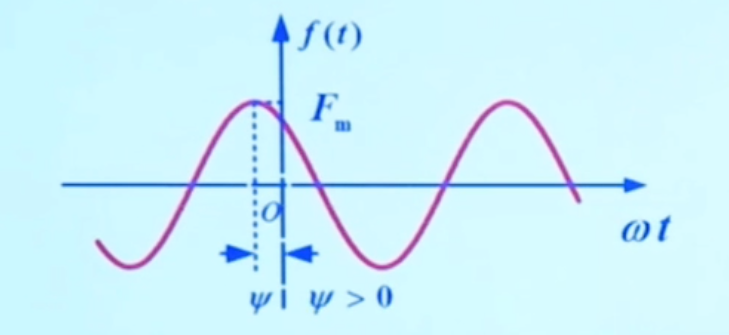 振幅,频率,初相统称为正弦量的三要素。
振幅,频率,初相统称为正弦量的三要素。
同频率正弦量的比较
两个同频率的正弦量:f1(t)=F1mcos(ωt+ψ1),f2(t)=F2mcos(ωt+ψ2)。
他们的相位差:ϕ=(ωt+ψ1)−(ωt+ψ2)=ψ1−ψ2。若 ϕ>0,则称 f1(t)超前f2(t)。反之则称 f1(t)滞后f2(t)。若 ϕ=0 则称二者同相。特殊的,当 ϕ=±π 时,我们称二者为反相,当 ϕ=±2π 时,我们称二者为正交。
同频率正弦量的运算
同频率正弦量的代数加、微分、积分 , 其结果仍为同频率的正弦量。只是幅度和相位发生了改变。
正弦量的相量
正弦量的相量表示
欧拉公式:ejθ+cosθ+jsinθ。我们用 ωt+ψ 代替 θ ,两边同时乘以常数 Fm,就能得到:Fmej(ωt+ψ)=Fmcos(ωt+ψ)+jsin(ωt+ψ)。其实部即为正弦量 f(t),所以我们可以表示为:
f(t)=Fmcos(ωt+ψ)=Re[Fmej(ωt+ψ)]=Re[Fmejψ+ejωt]=Re[F˙m⋅ejωt]
其中:F˙m=Fmejψ,简记为:F˙m=Fm∠ψ。F˙m=Fm∠ψ 是旋转向量 F˙m⋅ejωt 的复振幅。
所以对于一个电压正弦量(电流相同):
u(t)=2Ucos(ωt+ψu)↔U˙=U∠ψu(有效值向量)
基尔霍夫定律的相量形式
我们先写出 KCL 的时域形式:∑k=1Kik=0,我们使用相量来表示:
k=1∑Kik=k=1∑KRe[I˙kmejωt]=Re[k=1∑KI˙kmejωt]=Re[(k=1∑KI˙km)ejωt]=Re[(k=1∑K2I˙k)ejωt]=0
由此我们就可以得到 KCL 的向量形式:
k=1∑KI˙k=0
同理也可已得到 KVL 的向量形式:
k=1∑KU˙k=0
R, L, C 元件 VCR 的相量形式
电阻元件 VCR 的向量形式
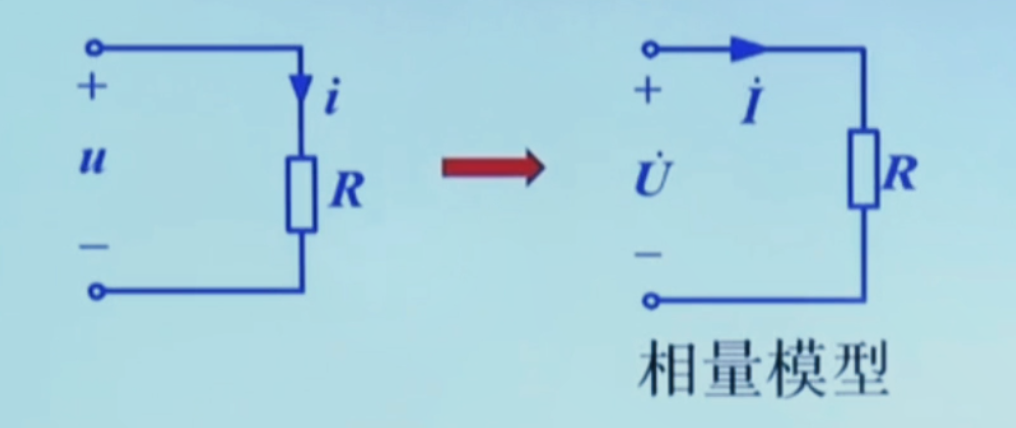 i(t)=Imcos(ωt+ψi)u=Ri=Re[2I˙ejωt]=Re[2I˙Rejωt]=Re[2U˙ejωt]
i(t)=Imcos(ωt+ψi)u=Ri=Re[2I˙ejωt]=Re[2I˙Rejωt]=Re[2U˙ejωt]
所以我们就可以得到电阻元件的 VCR 相量形式:
U˙=I˙R
进而我们可以推出:
U˙∠ψu=RI˙=RI∠ψi→{U=RIψu=ψi
即:电阻元件的电压与电流同相位。
电感元件 VCR 的向量形式
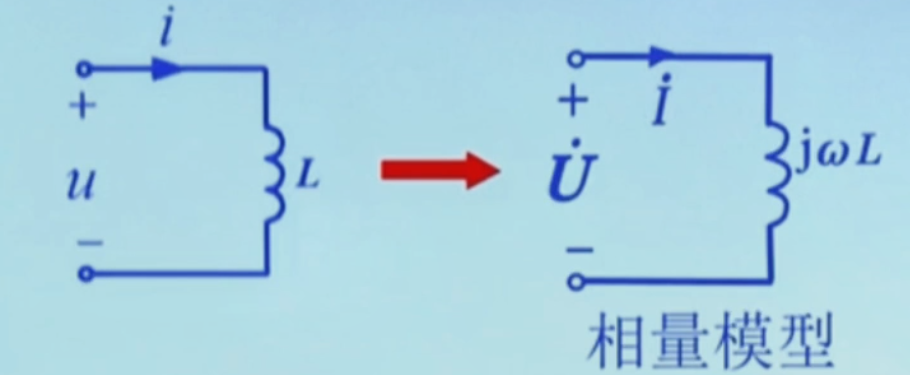 i(t)根据 VCR u(t)=Imcos(ωt+ψi)=Re[2iejωt]=Ldtdi=L⋅Re[2(jωI˙)ejωt]=Re[2(jωLI˙)ejωt]=Re[2U˙ejωt]
i(t)根据 VCR u(t)=Imcos(ωt+ψi)=Re[2iejωt]=Ldtdi=L⋅Re[2(jωI˙)ejωt]=Re[2(jωLI˙)ejωt]=Re[2U˙ejωt]
由此我们可以得出电感元件 VCR 的相量形式:
U˙=jωLI˙
进一步分析:
U˙=U∠ψu=jωLI˙=jωLI∠ψi=ωLI∠(ψi+90∘)→{U=ωLIψu=ψi+90∘
即:电感元件的电压超前电流 90∘。
电容元件 VCR 的相量形式
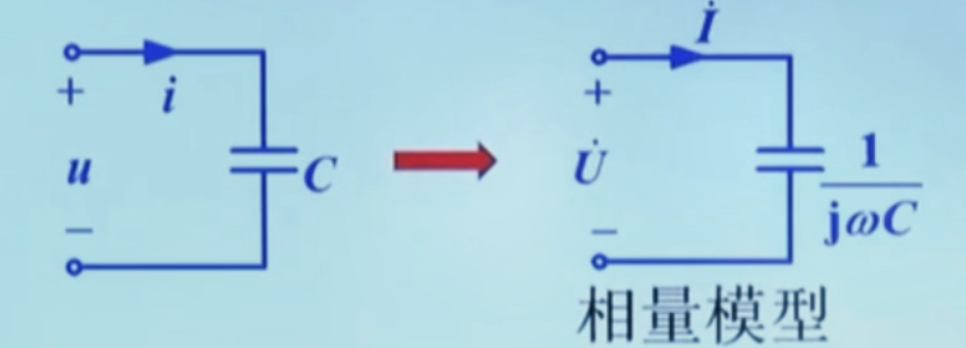 u(t)根据 VCR:i(t)=Umcos(ωt+ψu)=Re[2U˙ejωt]=Cdtdu=Cdtd{Re[2U˙ejωt]}=Re[2(jωCU˙)ejωt]=Re[2I˙ejωt]
u(t)根据 VCR:i(t)=Umcos(ωt+ψu)=Re[2U˙ejωt]=Cdtdu=Cdtd{Re[2U˙ejωt]}=Re[2(jωCU˙)ejωt]=Re[2I˙ejωt]
由此我们可以得出电容元件 VCR 的相量形式:
I˙=jωCU˙
进一步分析:
i=I∠ψi=jωCU˙=jωCU∠ψu=ωCU∠(ψu+90∘)→{I=ωCUψi=ψu+90∘
即:电容元件的电流超前电压 90∘。
欧姆定律的相量形式
将 R, L, C 元件相量形式的 VCR 重写如下:
U˙U˙LU˙C=RI˙R=jωRI˙L=jωC1I˙C
对比可以得出,这三个式子都可以用一个通式来表示:
U˙=ZI˙
这个通式就是欧姆定律的相量形式,其中,Z=I˙U˙,我们又称其为阻抗(单位与电阻相同)。同样的,我们又可以定义 Y=U˙I˙=Z1,称之为元件的导纳(单位与电导相同)。
R, L, C 元件的阻抗和导纳
阻抗
ZRZLZC=R=jωL=jωC1=−jωC1
阻抗的实部称为电阻,用符号 R 表示。阻抗的虚部称为电抗,用符号 X 表示。
对于电感元件来说:ZL=jωL 他只有虚部,所以电阻部分为零,只有电抗部分:XL=ωL。我们也称之为感抗,其与 ω 成正比。特殊的,当 ω=0 时,XL=0,这时候即为直流,我们称其为导直性质。
对于电容元件,与电感类似,我们将 XC=−ωC1 称为容抗,其与 ω 成反比。特殊的,当 ω=0 时,∣XC=∞∣,这时候即为开路,我们称其为隔直性质。
导纳
YRYLYC=R1=jωL1=−jωL1=jωC
导纳的实部称为电导,用符号 G 表示,虚部称为电纳,用符号 B 表示。
相似的,我们将电感元件的电纳 BL=−ωL1 称为感纳,电容元件电纳 BCωC= 称为容纳。
对于单个元件来说,阻抗和导纳是互为倒数的
单口网络的阻抗和导纳
以该电路为例,先画出他的向量模型:
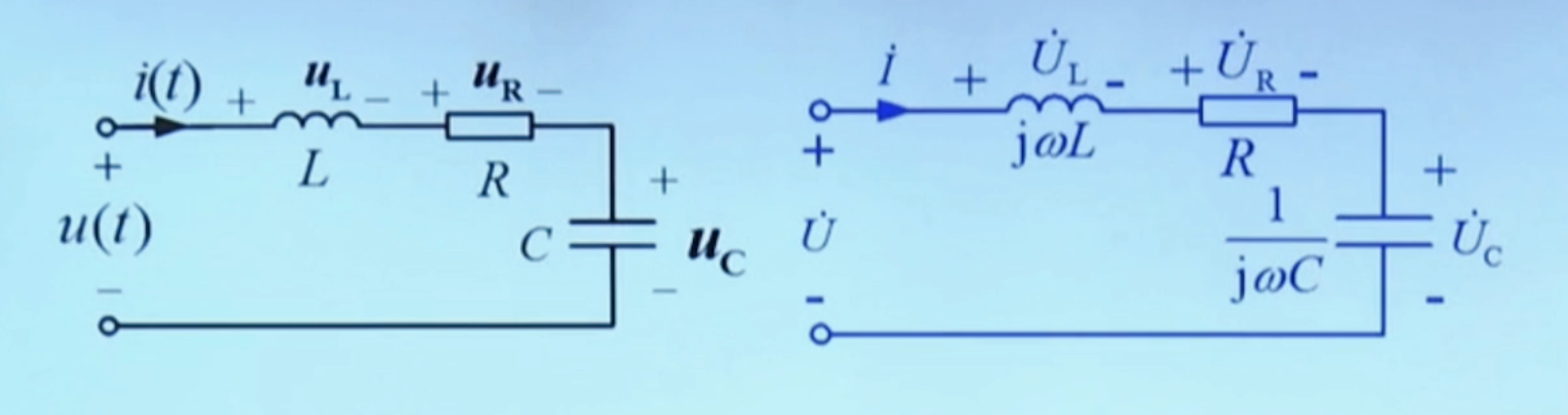 根据 KVL:
根据 KVL:
U˙=U˙L+U˙R+U˙C=jωLI˙+RI˙+jωC1I˙=(R+jωL−jωC1)I˙
单口网络的阻抗:
Z∣Z∣ψz=I˙U˙=R+jωL−jωC1=R+j(ωL−ωC1)=R+jX=∣Z∣∠ψz=z∠ψz=z=R2+X2——阻抗的模=arctanRX=arctan(RωL−ωC1)——阻抗的幅角(阻抗角)
所以,该单口网络的电阻分量:R, 电抗分量:X=ωL−ωC1。
我们有可以得到阻抗直角坐标形式与极坐标形式的关系:
R=∣Z∣cosψz=zcosψzX=∣Z∣sinψz=zsinψz
根据阻抗角的正负,我们也可以判断单口网络的性质:
ψz>0,电压超前电流,X>0 ——电感性电路ψz<0,电压滞后电流,X<0 ——电容性电路ψz=0,电压与电流同相位,X=0 ——电阻性电路
再来看该并联电路:
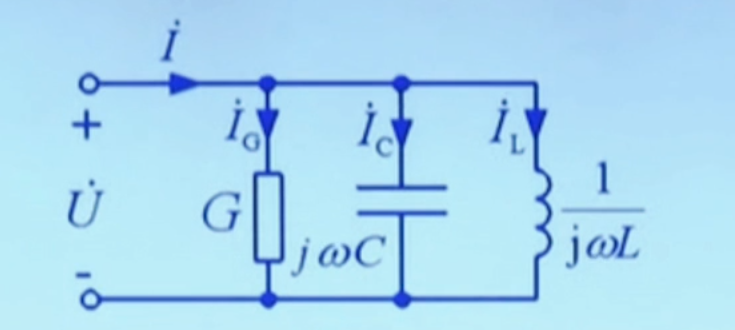 根据 KCL:
根据 KCL:
I=IG+IC+IL=GU˙+jωCU˙+jωL1U˙=(G+jωC−jωL1)U˙
单口网络的导纳:
Y=U˙I˙=G+jωC−jωL1=G+j(ωC−ωL1)=G+jB=∣Y∣∠ψY=y∠ψY
我们又可以得到:
∣Y∣ψy=y=G2+B2——导纳的模=arctanGB=arctan(GωC−ωL1)——导纳的幅角(导纳角)
所以,单口网络的电导为 G,电纳为:B=ωC−ωL1。
根据导纳角的正负也能判断电路性质:
ψYψYψY>0,电路呈电容性(电流超前电压)。<0,电路呈电感性(电流滞后电压)。=0,电路呈电阻性(电流电压同相位)。 振幅,频率,初相统称为正弦量的三要素。
振幅,频率,初相统称为正弦量的三要素。


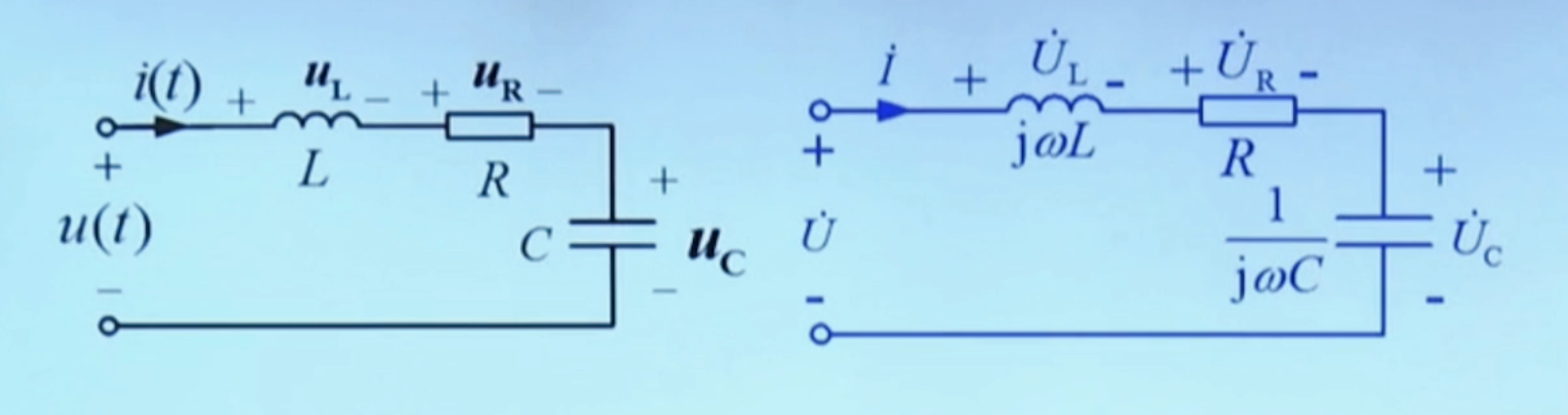 根据 KVL:
根据 KVL: 根据 KCL:
根据 KCL: