支路电流法&支路电压法
对于一个节点数为 n,支路数为 b 的电路,其 KCL 的独立方程个数为 n -1 个,而 KVL 独立方程个数为 b-n+1 个,共有 b 个方程,再加上其 b 条支路的 VCR 方程,则共有 2 b 个方程。即可通过解该 2 b 个方程来求得各支路电压与电流,这种方法为 2 b 法。
而我们想减少计算量,便将 VCR 方程代入至 KVL 方程中,就可以消去电压未知量,再与 KCL 方程联立,就可以得到 b 个电流变量的 b 个方程,便可以求出个支路电流,该方法为支路电流法 。
一旦求出各支路电流,便可以通过 VCR 来求得各支路电压。
相反的,将 VCR 带入到 KCL 方程中,就可以得到 b 个电压变量的 b 个方程,支路电流法解法类似,这种方法称为支路电压法 。
节点电压法
节点电压法是以节点电压以电路变量列写方程求解的一种分析方法。
基本思路 : 先选定一参考节点,然后对除参考节点以外的其他节点列 KCL 方程 , 根据各支路的 VCR, 用节点电压表示各支路电流,最后将用节点电压表示的各支路的 VCR 代入 KCL 方程 , 整理即得各节点的以节点电压为变量的方程。
以该电路为例:
{ i 1 + i 2 + i 3 = 0 − i 2 + i 4 + i 5 = 0 − i 3 − i 4 + i 6 = 0 \begin{cases}
i_{1}+i_{2}+i_{3} = 0 \\
-i_{2}+i_{4}+i_{5} = 0 \\
-i_{3}-i_{4}+i_{6} = 0
\end{cases} ⎩ ⎨ ⎧ i 1 + i 2 + i 3 = 0 − i 2 + i 4 + i 5 = 0 − i 3 − i 4 + i 6 = 0 同时写出个支路的 VCR 方程
{ i 1 = G 1 u 1 − i s 1 i 2 = G 2 u 2 i 3 = i s 3 i 4 = G 4 u 4 i 5 = G 5 u 5 i 6 = G 6 u 6 \begin{cases}
i_{1} = G_{1}u_{1}-i_{s1} \\
i_{2} = G_{2}u_{2} \\
i_{3} = i_{s3} \\
i_{4} = G_{4}u_{4} \\
i_{5} = G_{5}u_{5} \\
i_{6} = G_{6}u_{6}
\end{cases} ⎩ ⎨ ⎧ i 1 = G 1 u 1 − i s 1 i 2 = G 2 u 2 i 3 = i s 3 i 4 = G 4 u 4 i 5 = G 5 u 5 i 6 = G 6 u 6 写出支路电压与节点电压的关系:
u 1 = u n 1 u 2 = u n 1 − u n 2 u 3 = u n 1 − u n 3 u 4 = u n 2 − u n 3 u 5 = u n 2 u 6 = u n 3 \begin{align}
&u_{1}=u_{n1} \\
&u_{2}=u_{n1}-u_{n2} \\
&u_{3}=u_{n1}-u_{n3} \\
&u_{4}=u_{n2}-u_{n3} \\
&u_{5}=u_{n2} \\
&u_{6}=u_{n3}
\end{align} u 1 = u n 1 u 2 = u n 1 − u n 2 u 3 = u n 1 − u n 3 u 4 = u n 2 − u n 3 u 5 = u n 2 u 6 = u n 3 将这组关系带入到上方的 VCR 方程中,就可以得到以节点电压为变量的 VCR 方程。
{ i 1 = G 1 u n 1 − i s 1 i 2 = G 2 ( u n 1 − u n 2 ) i 3 = i s 3 i 4 = G 4 ( u n 2 − u n 3 ) i 5 = G 5 u n 2 i 6 = G 6 u n 3 \begin{cases}
i_{1}=G_{1}u_{n1}-i_{s1} \\
i_{2}=G_{2}(u_{n1}-u_{n2}) \\
i_{3}=is_{3} \\
i_{4}=G_{4}(u_{n2}-u_{n3}) \\
i_{5}=G_{5}u_{n2} \\
i_{6}=G_{6}u_{n3}
\end{cases} ⎩ ⎨ ⎧ i 1 = G 1 u n 1 − i s 1 i 2 = G 2 ( u n 1 − u n 2 ) i 3 = i s 3 i 4 = G 4 ( u n 2 − u n 3 ) i 5 = G 5 u n 2 i 6 = G 6 u n 3 将该 VCR 方程组带入到最开始的 KCL 方程中,就可以得到下面的方程组
{ ( G 1 + G 2 ) u n 1 − G 2 u n 2 − 0 = i s 1 − i s 3 − G 2 u n 1 + ( G 2 + G 4 + G 5 ) u n 2 − G 4 u n 3 = 0 0 − G 4 u n 2 + ( G 4 + G 6 ) u n 3 = i s 3 \begin{cases}
(G_{1}+G_{2})u_{n1}-G_{2}u_{n2}-0=i_{s1}-i_{s3} \\
-G_{2}u_{n1}+(G_{2}+G_{4}+G_{5})u_{n2}-G_{4}u_{n3}=0 \\
0-G_{4}u_{n2}+(G_{4}+G_{6})u_{n3}=i_{s3}
\end{cases} ⎩ ⎨ ⎧ ( G 1 + G 2 ) u n 1 − G 2 u n 2 − 0 = i s 1 − i s 3 − G 2 u n 1 + ( G 2 + G 4 + G 5 ) u n 2 − G 4 u n 3 = 0 0 − G 4 u n 2 + ( G 4 + G 6 ) u n 3 = i s 3 观察方程的左右,左边都是以节点电压为变量的组合,右边均为已知量。对于第一个方程的左侧来说,是从电阻流出节点 1 的电流代数和,右端是从电源流入节点 1 的电流代数和。后面的两个方程均有这种关系。
下面我们来写出具有四个节点的电路的节点电压方程的一般形式 (四个节点有三个节点电压方程,一个为参考节点) :
{ G 11 u n 1 + G 12 u n 2 + G 13 u n 3 = i s 11 G 21 u n 1 + G 22 u n 2 + G 23 u n 3 = i s 22 G 31 u n 1 + G 32 u n 2 + G 33 u n 3 = i s 33 \begin{cases}
G_{11}u_{n1}+G_{12}u_{n2}+G_{13}u_{n3}=i_{s11} \\
G_{21}u_{n1}+G_{22}u_{n2}+G_{23}u_{n3}=i_{s22} \\
G_{31}u_{n1}+G_{32}u_{n2}+G_{33}u_{n3}=i_{s33}
\end{cases} ⎩ ⎨ ⎧ G 11 u n 1 + G 12 u n 2 + G 13 u n 3 = i s 11 G 21 u n 1 + G 22 u n 2 + G 23 u n 3 = i s 22 G 31 u n 1 + G 32 u n 2 + G 33 u n 3 = i s 33 用矩阵来表示:
[ G 11 G 12 G 13 G 21 G 22 G 23 G 31 G 32 G 33 ] [ u n 1 u n 2 u n 3 ] = [ i s 11 i s 22 i s 33 ] \begin{equation}
\begin{bmatrix}
G_{11} & G_{12} & G_{13} \\
G_{21} & G_{22} & G_{23} \\
G_{31} & G_{32} & G_{33}
\end{bmatrix}
\begin{bmatrix}
u_{n1} \\
u_{n2} \\
u_{n3}
\end{bmatrix}
=
\begin{bmatrix}
i_{s11} \\
i_{s22} \\
i_{s33}
\end{bmatrix}
\end{equation} G 11 G 21 G 31 G 12 G 22 G 32 G 13 G 23 G 33 u n 1 u n 2 u n 3 = i s 11 i s 22 i s 33 对于矩阵中对角线元素我们用 G i i G_{ii} G ii G i j G_{ij} G ij i s i i i_{sii} i s ii G i i G_{ii} G ii G i j G_{ij} G ij
若电路中没有受控源,则 G i j = G j i G_{ij}=G_{ji} G ij = G ji
i s i i i_{sii} i s ii
特殊情况的列写
存在电压源与电阻串联的支路
将支路转化为电流源与电阻并联
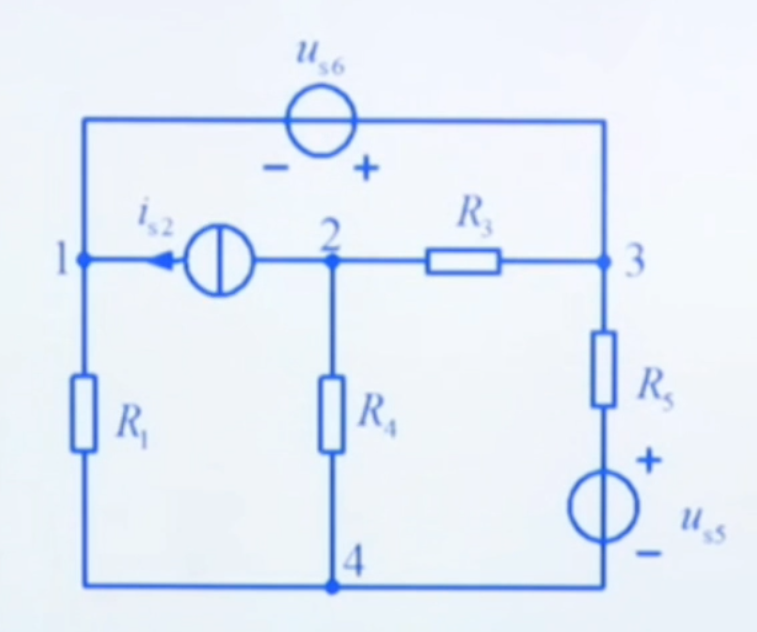
含有理想电压源支路(没有与电压源串联的电阻)
以该电路为例:
u s 6 u_{s6} u s 6 u s 6 u_{s6} u s 6 u s 6 = u n 3 − u n 1 u_{s6}=u_{n3}-u_{n1} u s 6 = u n 3 − u n 1
含有电流源与电阻串联的部分
如图:
( 1 R 1 + 1 R 2 ) u n 2 − 1 R 1 u n 1 − 1 R 2 u n 3 = − i s \left( \frac{1}{R_{1}} +\frac{1}{R_{2}}\right)u_{n2}-\frac{1}{R_{1}}u_{n1}-\frac{1}{R_{2}}u_{n3}=-i_{s} ( R 1 1 + R 2 1 ) u n 2 − R 1 1 u n 1 − R 2 1 u n 3 = − i s 电路中有受控源
此时,我们要把受控源当作独立源来对待,并把控制量用节点电压表示(即增加一个控制量与节点电压的关系方程)。
电路中有几个受控源,就要增加几个方程。
网孔电流法
网孔电流法是以网孔电流作为电路变量列写方程求解的一种方法。
基本思路 : 首先指定网孔电流方向 ; 然后对各网孔列写 KVL 方程 , 并根据各支路的 VCR, 将支路电压用网孔电流表示 ;最后将用网孔电流表示的各支路的 VCR 代入 KVL 方程 , 整理即得所求的网孔电流方程。
以该电路为例:
对这三个网孔列写 KVL 方程:
{ − u 1 + u 4 + u 6 = 0 − u 2 + u 4 + u 5 = 0 u 3 − u 5 + u 6 = 0 \begin{cases}
-u_{1}+u_{4}+u_{6}=0 \\
-u_{2}+u_{4}+u_{5}=0 \\
u_{3}-u_{5}+u_{6}=0
\end{cases} ⎩ ⎨ ⎧ − u 1 + u 4 + u 6 = 0 − u 2 + u 4 + u 5 = 0 u 3 − u 5 + u 6 = 0 写出各支路的 VCR 方程:
{ u 1 = R 1 i 1 − u s 1 u 2 = u s 2 + R 2 i 2 u 3 = u s 3 + R 3 i 3 u 4 = R 4 i 4 u 4 = R 5 i 5 u 6 = − u s 6 \begin{cases}
u_{1}= R_{1}i_{1}-u_{s1} \\
u_{2}=u_{s2}+R_{2}i_{2} \\
u_{3}=u_{s3}+R_{3}i_{3} \\
u_{4}=R_{4}i_{4} \\
u_{4}=R_{5}i_{5} \\
u_{6}=-u_{s6}
\end{cases} ⎩ ⎨ ⎧ u 1 = R 1 i 1 − u s 1 u 2 = u s 2 + R 2 i 2 u 3 = u s 3 + R 3 i 3 u 4 = R 4 i 4 u 4 = R 5 i 5 u 6 = − u s 6 再写出支路电流与网孔电流的关系
{ i 1 = − i m 1 i 2 = − i m 2 i 3 = i m 3 i 4 = i m 1 + i m 2 i 5 = i m 2 − i m 3 i 6 = i m 1 + i m 3 \begin{cases}
i_{1}=-i_{m1} \\
i_{2}=-i_{m2} \\
i_{3}=i_{m3} \\
i_{4}=i_{m1}+i_{m2} \\
i_{5}=i_{m2}-i_{m3} \\
i_{6}=i_{m1}+i_{m3}
\end{cases} ⎩ ⎨ ⎧ i 1 = − i m 1 i 2 = − i m 2 i 3 = i m 3 i 4 = i m 1 + i m 2 i 5 = i m 2 − i m 3 i 6 = i m 1 + i m 3 将这组方程带入到 VCR 方程中,就得到了用网孔电流来表示各支路电压的方程:
{ u 1 = − R 1 i m 1 − u s 1 u 2 = u s 2 − R 2 i m 2 u 3 = i s 3 + R 3 i m 3 u 4 = R 4 ( i m 1 + i m 2 ) u 5 = R 5 ( i m 2 − i m 3 ) u 6 = − u s 6 \begin{cases}
u_{1}=-R_{1}i_{m1}-u_{s1} \\
u_{2}=u_{s2}-R_{2}i_{m2} \\
u_{3}=i_{s3}+R_{3}i_{m3} \\
u_{4}=R_{4}(i_{m1}+i_{m2}) \\
u_{5}=R_{5}(i_{m2}-i_{m3}) \\
u_{6}=-u_{s6}
\end{cases} ⎩ ⎨ ⎧ u 1 = − R 1 i m 1 − u s 1 u 2 = u s 2 − R 2 i m 2 u 3 = i s 3 + R 3 i m 3 u 4 = R 4 ( i m 1 + i m 2 ) u 5 = R 5 ( i m 2 − i m 3 ) u 6 = − u s 6 再将这组方程带入到最初写的三个 kvl 方程中去进行整理:
{ ( R 1 + R 4 ) i m 1 + R 4 i m 2 + 0 = − u s 1 + u s 6 R 4 i m 1 + ( R 2 + R 4 + R 5 ) i m 2 − R 5 i m 3 = u s 2 0 − R 5 i m 2 + ( R 3 + R 5 ) i m 3 = − u s 3 + u s 6 \begin{cases}
(R_{1}+R_{4})i_{m1}+R_{4}i_{m2}+0=-u_{s1}+u_{s6} \\
R_{4}i_{m1}+(R_{2}+R_{4}+R_{5})i_{m2}-R_{5}i_{m3}=u_{s2} \\
0-R_{5}i_{m2}+(R_{3}+R_{5})i_{m3}=-u_{s3}+u_{s6}
\end{cases} ⎩ ⎨ ⎧ ( R 1 + R 4 ) i m 1 + R 4 i m 2 + 0 = − u s 1 + u s 6 R 4 i m 1 + ( R 2 + R 4 + R 5 ) i m 2 − R 5 i m 3 = u s 2 0 − R 5 i m 2 + ( R 3 + R 5 ) i m 3 = − u s 3 + u s 6 观察第一个方程的左端,是网孔 1 中电阻电位降的代数和,右端项为网孔 1 中电源电位升的代数和。对于其余两个方程同理。
对于具有三个网孔的电路的网孔电流方程的一般形式为:
{ R 11 i m 1 + R 12 i m 2 + R 13 i m 3 = u s 11 R 21 i m 1 + R 22 i m 2 + R 23 i m 3 = u s 22 R 31 i m 1 + R 32 i m 2 + R 33 i m 3 = u s 33 \begin{cases}
R_{11}i_{m1}+R_{12}i_{m2}+R_{13}i_{m3}=u_{s11} \\
R_{21}i_{m1}+R_{22}i_{m2}+R_{23}i_{m3}=u_{s22} \\
R_{31}i_{m1}+R_{32}i_{m2}+R_{33}i_{m3}=u_{s33}
\end{cases} ⎩ ⎨ ⎧ R 11 i m 1 + R 12 i m 2 + R 13 i m 3 = u s 11 R 21 i m 1 + R 22 i m 2 + R 23 i m 3 = u s 22 R 31 i m 1 + R 32 i m 2 + R 33 i m 3 = u s 33 该方程组中共有三个要素:
R i i R_{ii} R ii R i j R_{ij} R ij 如果将各网孔的电流的方向设为同一绕行方向,则互阻总为负。
当电路中没有受控源时,R i j = R j i R_{ij}=R_{ji} R ij = R ji
u s i i u_{sii} u s ii
特殊情况的列写
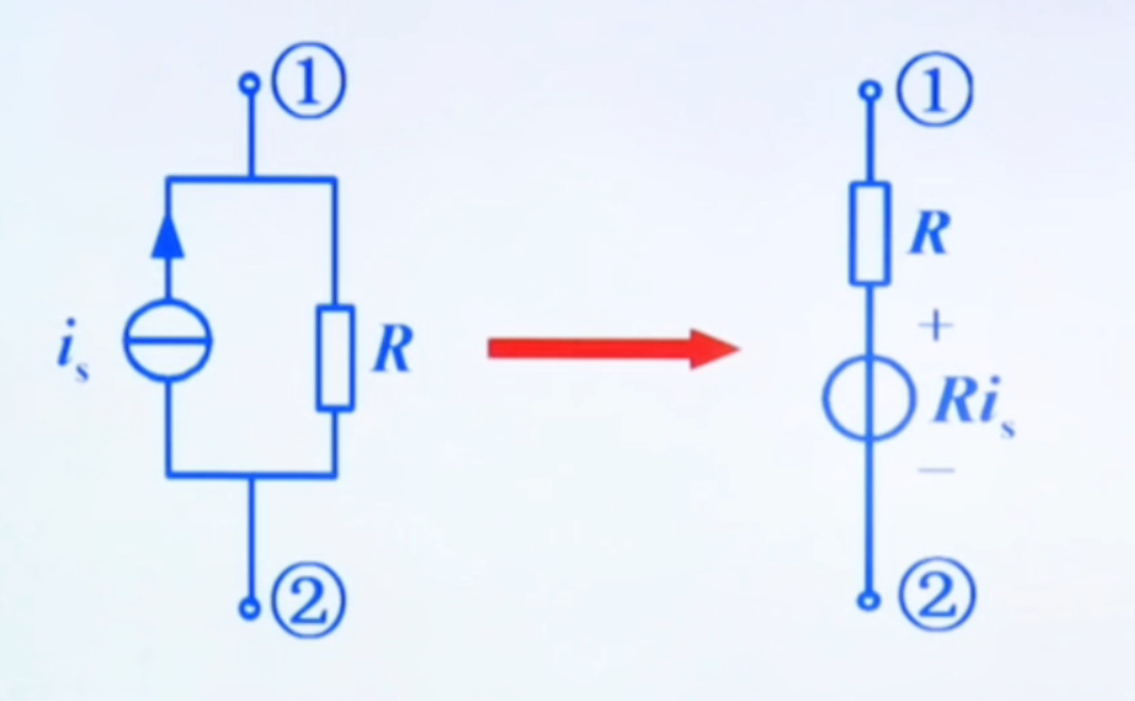
含有电流源与电阻并联的支路
将支路转化为电压源与电阻串联
含有理想电流源支路(没有与之并联的电阻)
此时一般有两种情况:
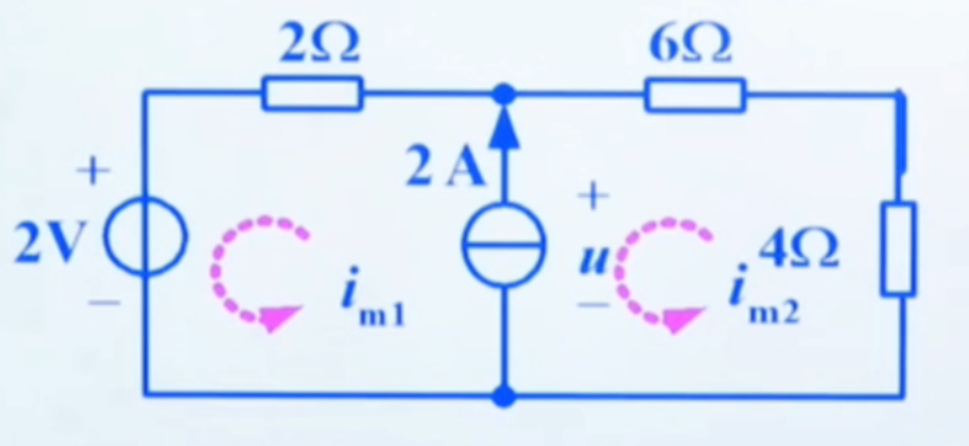
(a):只有一个网孔电流通过理想电流源支路,此时,该网孔电流已知,即为电流源电流。
(b):电流源支路是两个网孔的公共支路,此时,要先假设电流源所在支路电压为一个未知量,并在列方程时当作电压源电压对待。同时增列一个电流源支路电流与相关网孔电流的方程。
对于所示电路,即为:2 A = i m 1 − i m 2 2A=i_{m1}-i_{m2} 2 A = i m 1 − i m 2
含有电压源与电阻并联的支路
以该电路为例:
( R 2 + R 3 ) i m 2 − R 3 i m 1 = u s (R_{2}+R_{3})i_{m2}-R_{3}i_{m1}=u_{s} ( R 2 + R 3 ) i m 2 − R 3 i m 1 = u s
电路中有受控源
把受控源当作独立源对待,并把控制量用网孔电流表示(即增加一个控制量与网孔电流的关系方程)。
电路中有几个受控源,就要增加几个方程。
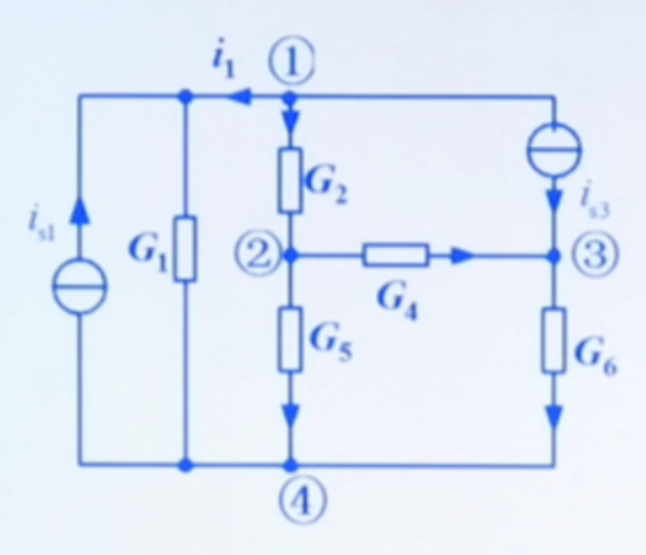 选择节点 4 为参考节点,列出其余节点的 KCL 方程。
选择节点 4 为参考节点,列出其余节点的 KCL 方程。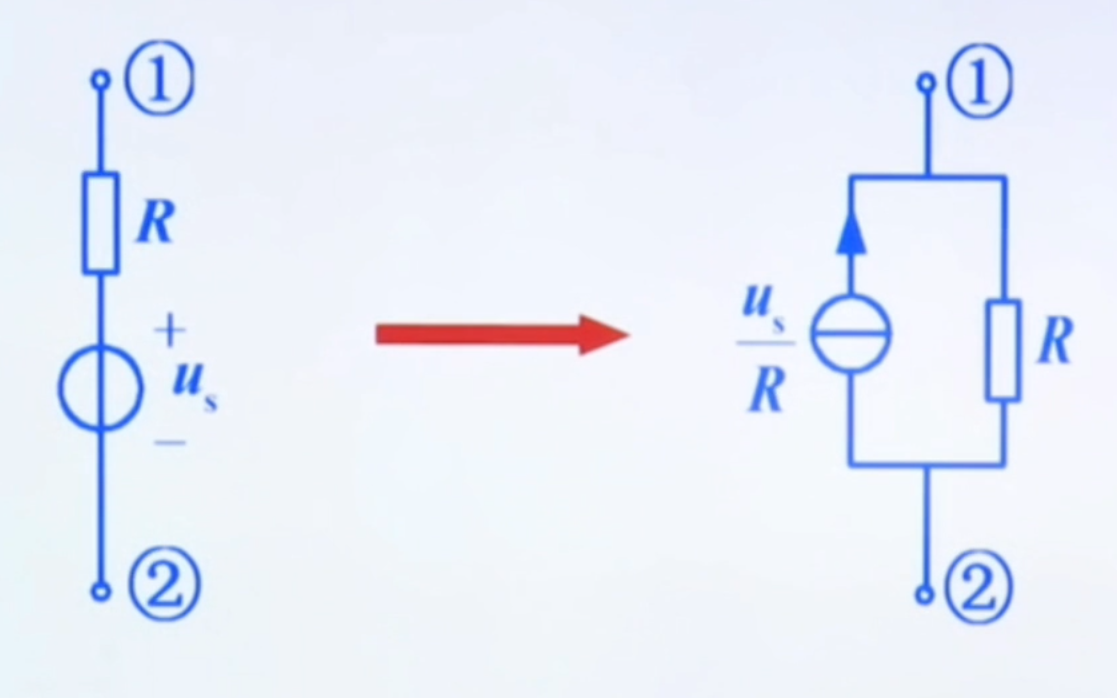
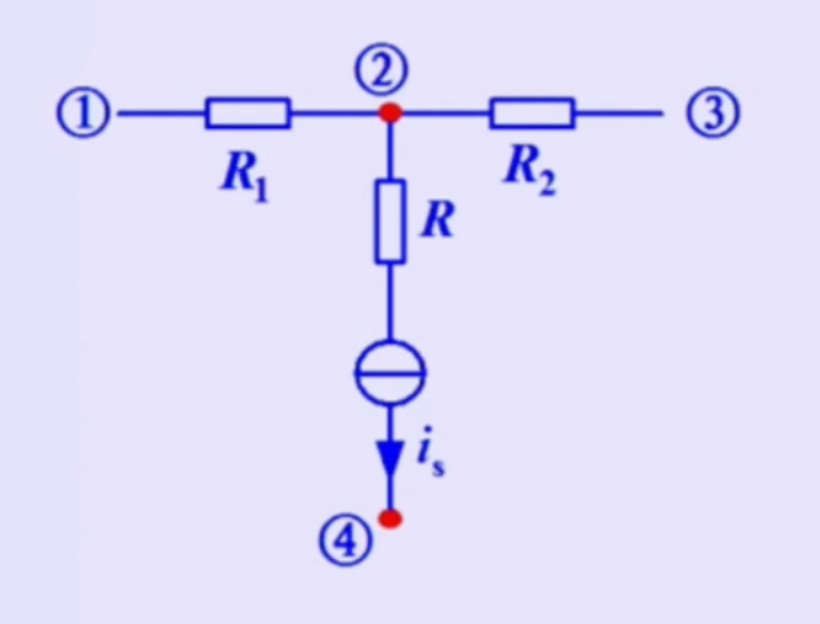 对与该电路在列节点 2 与节点 4 的方程时,与电流源串联的电阻 R 是不考虑的(R 对节点 2 是没有贡献的),所以对于节点 2 可以列出如下方程:
对与该电路在列节点 2 与节点 4 的方程时,与电流源串联的电阻 R 是不考虑的(R 对节点 2 是没有贡献的),所以对于节点 2 可以列出如下方程: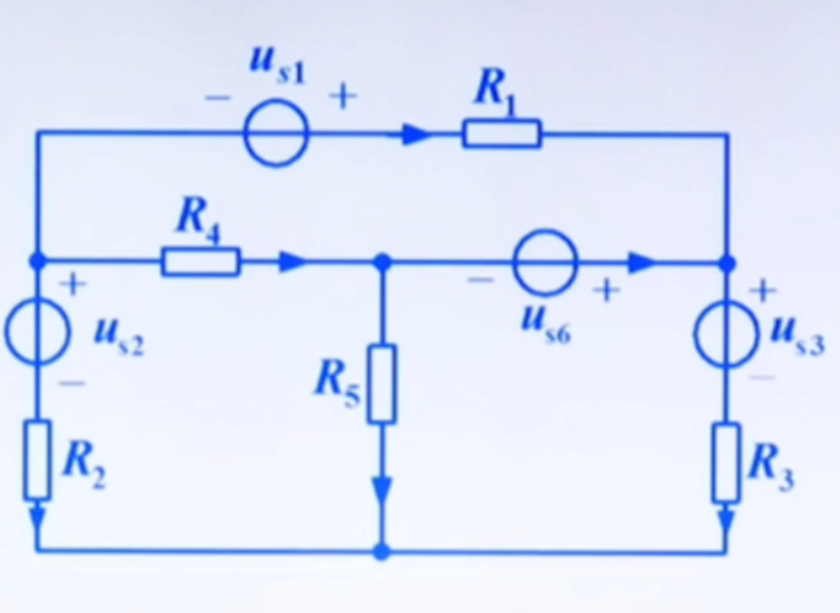 画出该电路的图:
画出该电路的图:
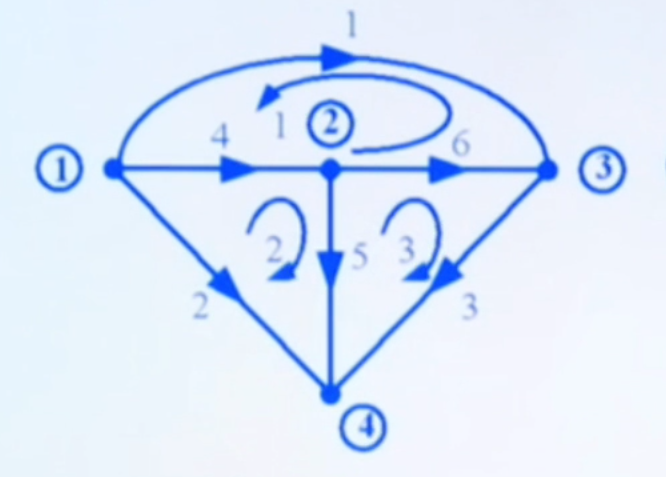
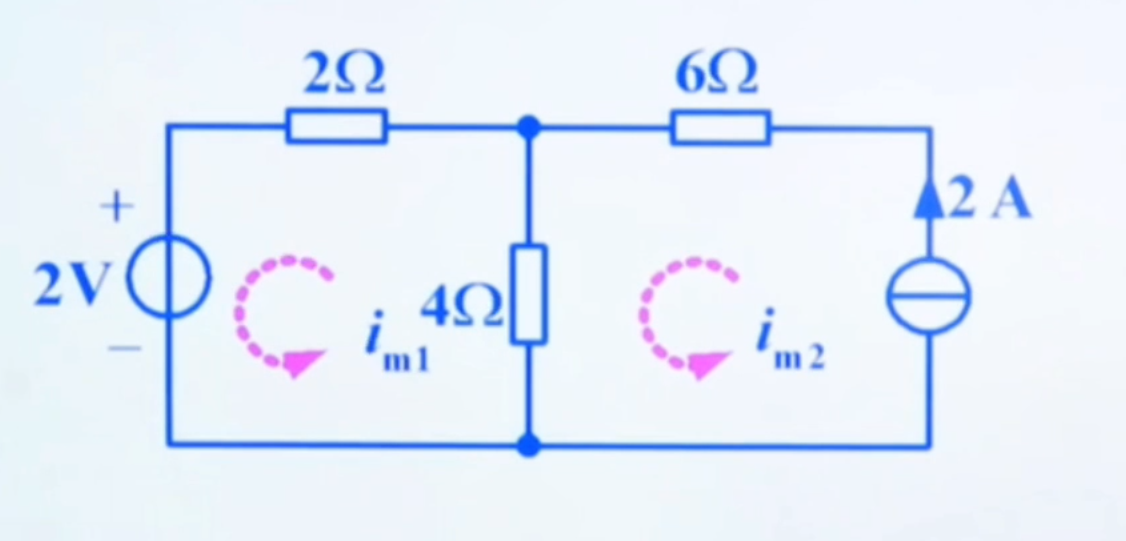
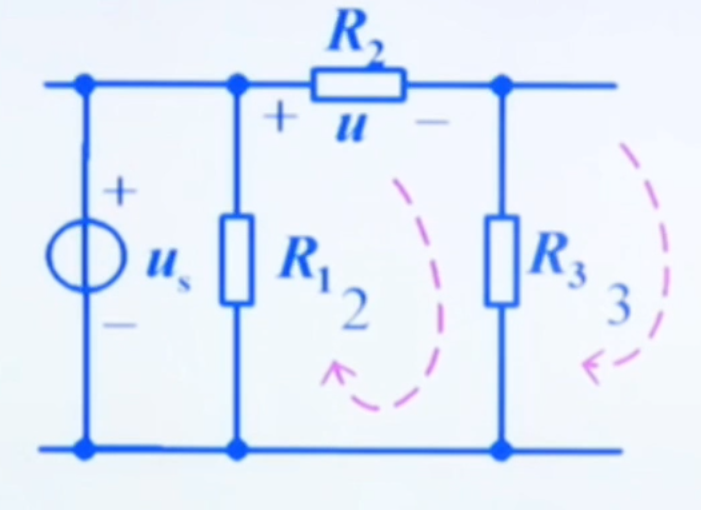 此时,在列写方程时,电阻 R 1 是不考虑的(R 1 对网孔 2 无贡献)。所以对于网孔 2 所列方程为
此时,在列写方程时,电阻 R 1 是不考虑的(R 1 对网孔 2 无贡献)。所以对于网孔 2 所列方程为